


Next: Efter de allmänna
Up: Den historiska utvecklingen
Previous: Greker och araber
I norditalien på 1500-talet upptäcktes formler för lösningarna av
tredje- och fjärdegradsekvationerna. Detta skedde under det att
kraftiga konflikter uppstod. De inblandade personerna var
Scipione del Ferro (1465--1526), Tartaglia (vilket betyder
stammaren, egentligen hette han Niccolò Fontana) (1499--1557),
Geronimo Cardano (1501--1576) och Lodovico Ferrari
(1522--1565). Upptäckten av dessa lösningar var väsentligen det första
överträffandet av vad grekerna och araberna hade
uträttat. Överträffandet av deras gamla resultat fick stor psykologisk
effekt och banade väg för nya upptäckter inom matematiken.
En anledning till att konflikter uppstod är att man på den tiden inte
snabbt publicerade sina resultat för att få sitt namn inskrivet i
historieböckerna. Istället hemlighöll man ofta sina resultat, som ett
slags trumfkort eller trolleritrick. Den förste som löste den
allmänna tredjegradsekvationen var del Ferro, det finns omvittnat och
nedskrivet av Ferrari och nämns också av Cardano i '' Ars
Magna'' som finns i engelsk översättning [1]. Han
gjorde det omkring år 1515 då han var professor vid universitetet i
Bologna. Lösningen lämnade han, enligt den pythagoreiska traditionen,
under tysthetslöfte till sina elever. En av eleverna, Antonio
Maria Fior från Venedig, använde denna kunskap till att utmana
Tartaglia i en tävling år 1535. Detta fick Tartaglia att anstränga sig
till det yttersta, och han lyckades lösa alla uppgifterna i tävlingen
(vilket Fior inte gjorde). Han har troligtvis därmed, oberoende av del
Ferro, löst den allmänna tredjegradsekvationen. Detta gjorde Cardano
mycket intresserad. Efter vissa turer, inklusive ett löfte om att
bevara lösningsmetoden hemlig (enligt Tartaglia), fick han till sist
reda på lösningen och hjälp att förstå den av Tartaglia. Trots
tysthetslöftet offentliggjorde Cardano år 1545 lösningen av
tredjegradsekvationen, med Tartaglia angiven som
upphovsman, i sin bok Ars Magna. Samtidigt nämns att det var del
Ferro som gjorde den första lösningen. Detta ledde till ett långt och
våldsamt gräl mellan Tartaglia och Ferrari (som försvarade Cardano),
emedan Cardano höll sig ganska passiv.
Den förste att lösa den allmänna fjärdegradsekvationen var Cardanos
elev Ferrari, som överträffade sin lärare genom detta när han själv
var 23 år. Den lösningen finns också i Ars Magna, där 20 olika fall
diskuteras. Dessa fall kallas de mest allmänna och Cardano nämner att
det finns 67 andra fall. Anledningen till uppdelningen i olika fall
var mestadels att att bevisen bygger på geometri och därför betraktas
endast positiva koefficienter.
Den s.k. Cardanos formel för rötterna till en tredjegradsekvation
borde alltså egentligen heta del Ferros formel. I vissa fall
producerar formlerna reella lösningar som summan eller skillnaden av
komplexa tal, detta kunde Cardano ej tolka. Cardano noterade dock att
det ibland blev negativa tal under rottecknet, t ex när han försökte
lösa 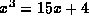 och han visste att en lösning är x=4. Han skrev
till Tartaglia den 4 augusti 1539 om detta problem, men Tartaglia
kunde inte heller förklara det. Raffael Bombelli (1526--1573)
publicerade dock i sin bok Algebra år 1572 ett sätt att
räkna med komplexa tal, vilket gjorde det möjligt att förklara
fallet
och han visste att en lösning är x=4. Han skrev
till Tartaglia den 4 augusti 1539 om detta problem, men Tartaglia
kunde inte heller förklara det. Raffael Bombelli (1526--1573)
publicerade dock i sin bok Algebra år 1572 ett sätt att
räkna med komplexa tal, vilket gjorde det möjligt att förklara
fallet 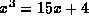 . Bombellis förklaring bygger dock på att man vet
att x=4 är en lösning.
. Bombellis förklaring bygger dock på att man vet
att x=4 är en lösning.



Next: Efter de allmänna
Up: Den historiska utvecklingen
Previous: Greker och araber
Peter Johansson
Thu Mar 28 16:15:01 MET 1996
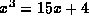 och han visste att en lösning är x=4. Han skrev
till Tartaglia den 4 augusti 1539 om detta problem, men Tartaglia
kunde inte heller förklara det. Raffael Bombelli (1526--1573)
publicerade dock i sin bok Algebra år 1572 ett sätt att
räkna med komplexa tal, vilket gjorde det möjligt att förklara
fallet
och han visste att en lösning är x=4. Han skrev
till Tartaglia den 4 augusti 1539 om detta problem, men Tartaglia
kunde inte heller förklara det. Raffael Bombelli (1526--1573)
publicerade dock i sin bok Algebra år 1572 ett sätt att
räkna med komplexa tal, vilket gjorde det möjligt att förklara
fallet 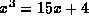 . Bombellis förklaring bygger dock på att man vet
att x=4 är en lösning.
. Bombellis förklaring bygger dock på att man vet
att x=4 är en lösning.