
Join the Blue Ribbon Anti-Censorship Campaign!
You are visitor number 12610 since November 2019.
Last update: April 2005
How are the maps generated?
The algorithm I use was designed by Voss, and one can call it "Voss fractal faulting algorithm". The idea is that you take a sphere, bisect (cut it in two equal parts) with a plane, take one of the hemispheres and elevate or declinate it. This is called one fault. Then you generate another fault, slices and elevate/declinate. The number of faults is the same as the number of iterations.
What has this to do with the figure above?
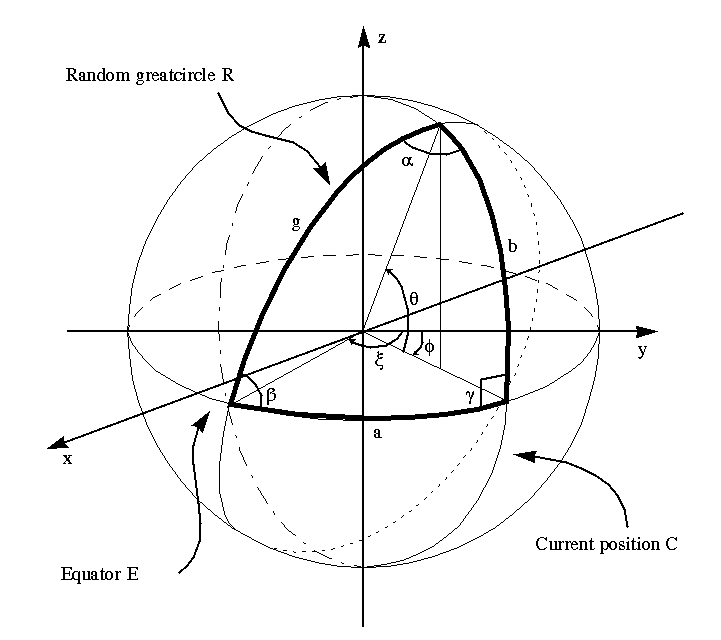
If you want to implement the algorithm above, you need to describe it in mathematical terms, and I've put the picture above to simplify the description of how it's done.
I want to generate a flat projected map, since it's much easier to handle a rectangular array then a spherical surface. Now you want an easy way to describe which part of this array you should elevate/declinate. One way of doing this is to use something called greatcircles. A greatcircle is a circle that lies on the surface of a sphere and has the same radius as the sphere. A wellknown example of this is the earths equator, which divides the earth in a northern and southern hemisphere.
How can you descirbe describe a greatcircle on a flatprojection of a sphere?
I don't know if this is the optional way of describing the flat projection of a greatcircle, so if you know a better way, I would be very delighted if you could tell me! :)
Take a look at the picture now. What you see a righthand system with a spere centered in origo. I have drawn three greatcircles, the Equator E, the Current position C and the Random greatcircle R. These greatcircles together describe several spherical triangles of which I have choosen one. The sides of this spherical triangle is called a, b and g. A function which describes a flatprojected greatcircle gives the distance b (the latitude of a point on the greatcircle) from the equator at the current position Phi. You can find this distance by solving the spherical triangle for the side b, which is the same as the angle Theta, since we are using a unit sphere. By using two of Napier's equations for spherical triangles:
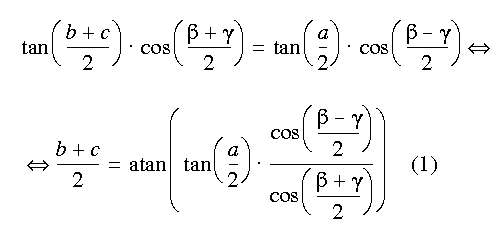 and
and
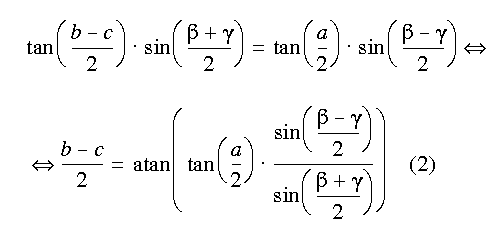 By combining (1) and (2), using some trigonometric relations and simplifying the expression one get the following:
By combining (1) and (2), using some trigonometric relations and simplifying the expression one get the following:
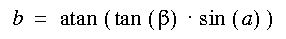 What's left is to find expressions for ß and a. In the formulas below i, j and k stands for how much the "equator" is rotated around the x-, y- and z-axis...
What's left is to find expressions for ß and a. In the formulas below i, j and k stands for how much the "equator" is rotated around the x-, y- and z-axis...
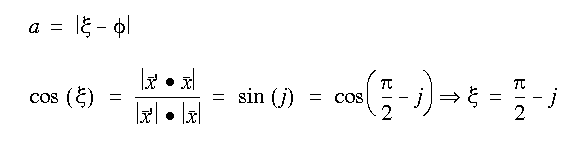 and
and
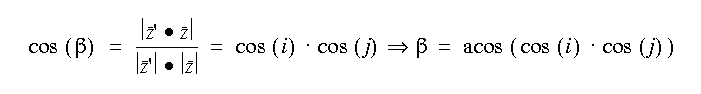 where
where
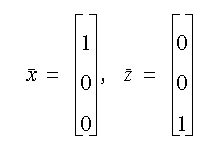 and j and i comes from
and j and i comes from
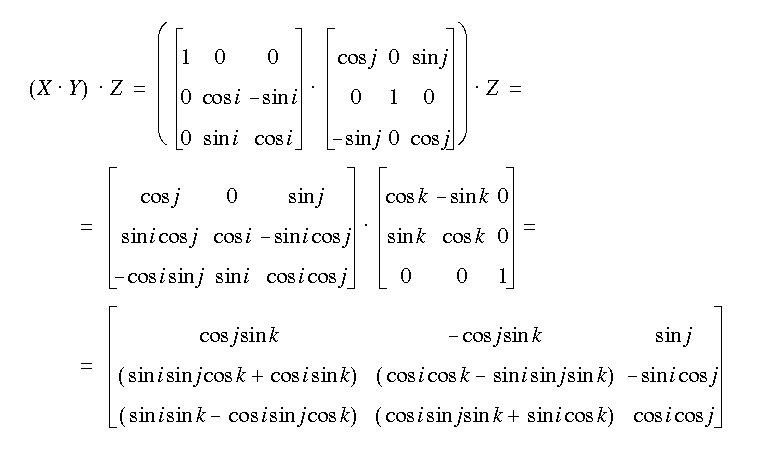 X describes rotation round the x-axis, Y describes rotation round the y-axis and Z describes rotation round the z-axis.
If you have made it this far, I hope you'll understand why it takes so long time to compute the maps! :)
X describes rotation round the x-axis, Y describes rotation round the y-axis and Z describes rotation round the z-axis.
If you have made it this far, I hope you'll understand why it takes so long time to compute the maps! :)
 Back to the generator.
Back to the generator.
Last update: April 2005 CET by John Olsson
 Graphics created with Pixelsight
Graphics created with Pixelsight
![]()


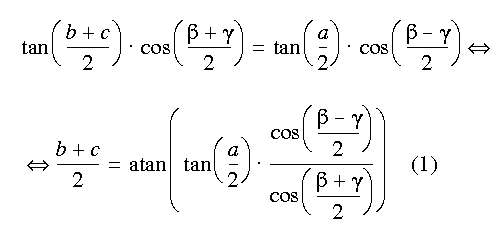 and
and
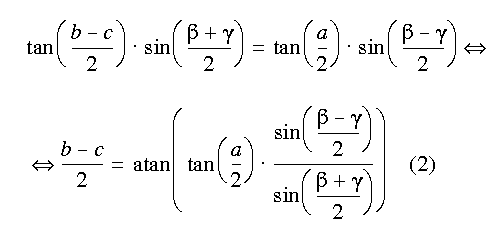 By combining (1) and (2), using some trigonometric relations and simplifying the expression one get the following:
By combining (1) and (2), using some trigonometric relations and simplifying the expression one get the following:
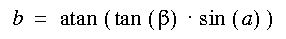 What's left is to find expressions for ß and a. In the formulas below i, j and k stands for how much the "equator" is rotated around the x-, y- and z-axis...
What's left is to find expressions for ß and a. In the formulas below i, j and k stands for how much the "equator" is rotated around the x-, y- and z-axis...
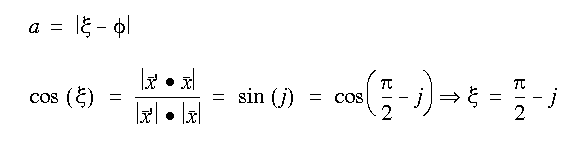 and
and
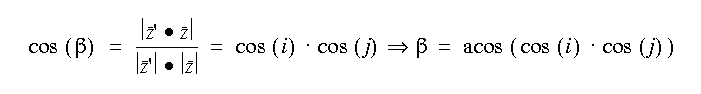 where
where
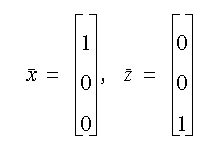 and j and i comes from
and j and i comes from
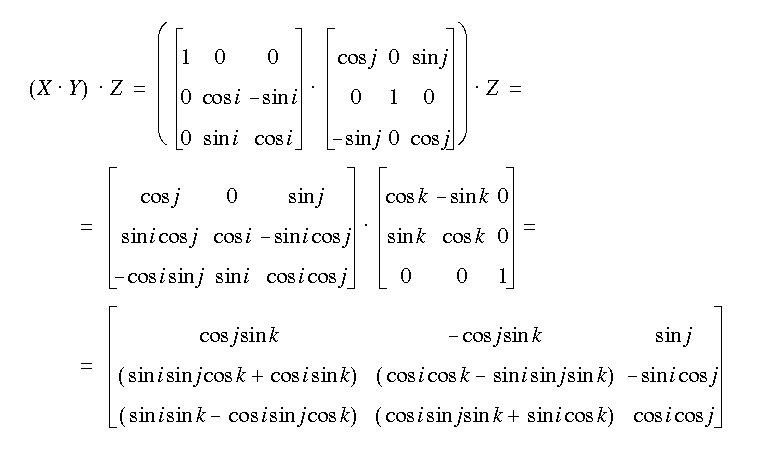 X describes rotation round the x-axis, Y describes rotation round the y-axis and Z describes rotation round the z-axis.
If you have made it this far, I hope you'll understand why it takes so long time to compute the maps! :)
X describes rotation round the x-axis, Y describes rotation round the y-axis and Z describes rotation round the z-axis.
If you have made it this far, I hope you'll understand why it takes so long time to compute the maps! :)